Равенство двух отношений

Основные учебники математики, которые используют в младших классах

Петерсон. По этой системе занимаются большинство школ с «сильной» математикой. В учебнике нет объяснений и правил, зато представлены разные типы задач, в том числе и на смекалку. Приверженцы системы говорят о том, что она учит мыслить нестандартно. Противники считают учебник путаным и бессистемным.

Моро. Базовый учебник для большинства школ, много заданий на развитие вычислительных способностей детей, примеров и типовых задач.

Гейдман. Учебник с большим количеством нетиповых заданий, а также с правилами и объяснениями. Боле сложный, чем Моро, лучше структурирован и консервативней системы Петерсон.

Петерсон (3-й класс)

Бабушке надо зажарить 6 котлет, а на сковородке умещается только 4 котлеты. Каждую котлет надо жарит 5 мину на одной стороне и 5 минут на другой. За какое минимальное время бабушка зажарит все котлеты?

Обычно жарят так: кладут 4 котлеты, жарят 5 минут, переворачивают и жарят еще 5 минут; затем кладут еще 2 котлеты и все повторяют в том же порядке. На все это потребуется 20 минут. Однако можно потратить еще меньше времени. Сначала жарим 5 минут четыре котлеты с одной стороны. Затем две котлеты переворачиваем, а две другие заменяем сырыми. Жарим еще 5 минут. Две обжаренные с двух сторон котлеты заменяем полупрожаренными, а две другие переворачиваем и жарим еще 5 мину. При такой жарке потребуется 15 минут.

Петерсон (3-й класс)

Крестьянин пришел к царю и попросил: «Царь, позволь мне взять одно яблоко из твоего сада». Царь разрешил. Пошел крестьянин к саду и видит: весь сад огорожен тройным забором, в каждом заборе есть только одни ворота, и около каждых ворот стоит сторож. «Царь разрешил мне взять одно яблоко из сада», — сказал крестьянин первому сторожу. «Возьми, но при выходе отдашь мне половину тех яблок, которые у тебя будут, и еще одно», — ответил сторож. То же сказали и другие сторожа, охранявшие ворота. Сколько яблок должен взять крестьянин, чтобы, отдав положенные части трем сторожам, унеси домой одно яблоко?

Первый способ решения — арифметический. Рассуждаем с конца задачи. У крестьянина осталось 1 яблоко перед этим он отдал 1 яблоко, значит, у него было 1 + 1, но это была половина, тогда (1 + 1)×2 — столько яблок у крестьянина было, когда он подошел к последнему сторожу. Второму сторожу крестьянин отдал 1 яблоко, значит, у него было (1 + 1)×2 + 1 и еще половину ((1 + 1)×2 + 1)×2. Аналогичная ситуация произошла при встрече крестьянина с первым сторожем. Таким образом, он должен был взять в саду (((1 + 1)×2 + 1)×2 + 1) × 2 = 22 (ябл.)

Второй способ — алгебраический. Пусть x яблок крестьянин взял в саду, подойдя к первому сторожу, он отдал х : 2 — половину и еще одно, значит, х : 2 – 1. Второму сторожу он отдал половину (х: 2 – 1) : 2 и еще одно, значит, (х : 2 – 1) : 2 – 1. Третьему сторожу он отдал половину и еще одно, то ест ((х : 2 – 1): 2 – 1) : 2 – 1. Зная, что у него осталось 1 яблоко, составим уравнение ((х : 2 – 1): 2 – 1) : 2 – 1 = 1.

Третий способ — с помощью обратных операций, оформить можно в виде линейного выражения, записать обратные операции и вычислить его значение.

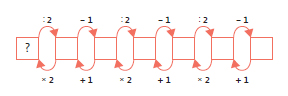
Для учеников решение данной задачи с помощью схемы с использованием обратных операций оказалось наиболее понятным.

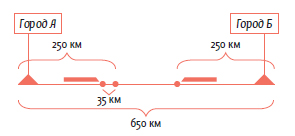
Из двух городов, расстояние между которыми 650 км, вышли навстречу друг друг два поезда. Один прошел 250 км, а другой — на 35 км меньше. На каком расстоянии друг от друга находятся поезда?

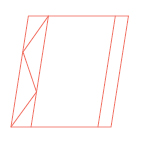
Нарисуй такую папку для бумаг, не отрыва карандаш от бумаги. Проводить линию карандашом можно только один раз.